Physical oceanography: Partial derivatives

Why do you need to learn partial derivatives to understand what’s going on in the ocean?

Partial derivatives can tell us how temperature changes over time, distance and depth. This is part of environmental fluid mechanics focusing on ocean circulation and the physical processes driving waves and currents.

Climate change is largely about temperatures. Rising temperatures affects coral reefs survival, fish search for food, algaes, the forming of hurricanes and melting of ice caps and shelfs.

I turn to Karnauskas who writes: “Did you forget what a partial derivative is? No problem! Even if you have taken years of partial differential equation (PDE) courses, you may not be accustomed to applying them in an Earthly context and so you, too, could use a little practice evaluating them by eye.”

This is good, I think. Not only can I learn what it is, but also why they are relevant for physical oceanography.

Back to Karnauskas’ book: “Partial differentiation is about acknowledging that we live in a four-dimensional world (including time), but only thinking about one dimension at a time. Specifically, the qualifier “partial” simply means the rate of change of a variable with respect to only one dimension (holding all others constant), and at just one place and time.“

What is a derivative?

For a function of one independent variable, say x, the derivative gives information about how the function, say f(x), changes when x changes.  This is the meaning of the first derivative. Geometrically, it’s the slope of a tangent line (red line in figure below).

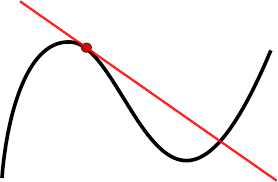
I found one understandable way of explaining it in Calculus Refresher.

“Calculus, very simply, is concerned with change. It explains how fields (ocean temperature, salinity, velocity, etc.) change along a certain dimension. For most geophysical purposes, we are concerned with changes of these fields along the space and time dimensions. Representing the evolution of the fields in a mathematical form (as partial differential equations) allows the following. 1) prove or disprove the mechanisms that drive oceanic flows and 2) explain and/or predict behavior in the ocean.”

Vector

As described by Karnauskas, we live in a three-dimensional world (as in the Cartesian dimensions x, y and z). This means seawater at any particular location might be moving a little bit eastward, southward, too, and sinking all at the same time. Constituting both a speed and direction, vectors are useful for describing fluid velocity.

If it helps, if not completely comparable, mosquitos are vectors of malaria. In other words, vectors carry something in a direction. It’s the combination of partial derivatives.

I can understand this. Now, it’s time to grasp a few mathematical symbols used to express this which is explained in this video:

As I read about this, and slowly grasp what this means in practical terms, I look forward to understanding how velocity divergence and curl are used to understand ocean circulation.

The next page turner phrase by Karnauskas is: “Let’s try to understand what makes the ocean tick, how it interacts with the atmosphere, and how it all fits into global variability and change.”

Featured image: Saltstraumen; the world’s strongest tidal current.